(ResNet)Deep Residual Learning for Image Recognition[2015]
思路
本文的主要贡献在于让更深的网络模型的效果不下降
问题发现
在以往的工作中，大家都在尝试让网络层数更深，来获得更好的效果，然而作者发现随着层数的增加，效果会反而降低。
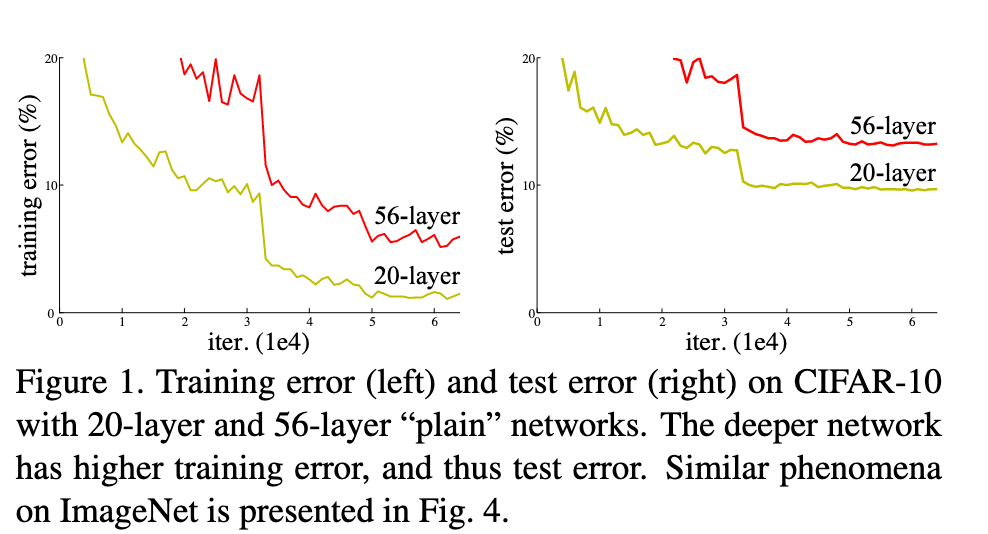出乎意料的是，这种退化并不是由过度拟合引起的，并且在适当深度的模型中添加更多层会导致更高的训练误差
问题分析
考虑在原来好效果的模型之上添加新的层，如果这些层是恒等映射(identity mapping),它们不会对原有模型有任何影响所以会保持原来的效果。如果这些新层学习到了新知识，整个网络的效果应该更好或者至少不下降，但是试验表明目前的方法不能达到更好的效果(或者需要过大的计算开销)
本文的解决方法就是显式地让这些新的层去学习恒等映射而不是直接堆叠连接
假设我们的理想映射是 $\mathbf{H}(\mathbf{x})$ ,让叠加的新层学习 $\mathbf{F}(\mathbf{x}) = \mathbf{H}(\mathbf{x}) - \mathbf{x}$ 则原始的映射就表示为 $\mathbf{H}(\mathbf{x}) = \mathbf{F}(\mathbf{x}) +\mathbf{x}$
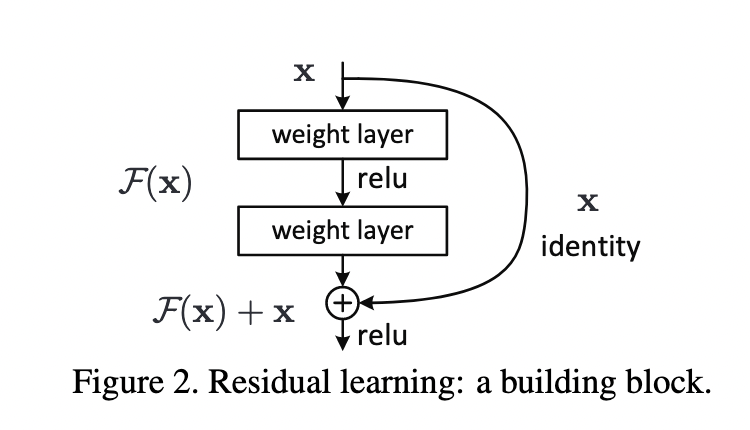在极端情况下，如果恒等映射是最优的，则将新层置为零比通过一堆非线性层拟合恒等映射更容易
模型(Deep Residual Learning)
残差学习(Residual Learning)
短路实现恒等映射(Identity Mapping by Shortcuts)
残差块的公式如下：
$$
{\bf y}=\mathcal{F}({\bf x},\{W_{i}\})+{\bf x}.
$$
其中${\bf x}，{\bf y}$ 是输入输出，$\mathcal{F}({\bf x},\{W_{i}\})$代表了需要学习的残差映射
方程中的快捷连接既不引入额外的参数，也不引入额外的计算复杂性。这不仅在实践中有吸引力，而且在我们比较普通网络和残差网络时也很重要。
要求 $\mathcal{x}$和 $\mathcal{F}$ 的维度要一致，如果不一致，需要将 $\mathcal{x}$ 进行投影， $W_{s}$仅在匹配尺寸时使用 $$ {\bf y}=\mathcal{F}({\bf x},\{W_{i}\})+W_{s}{\bf x}. $$
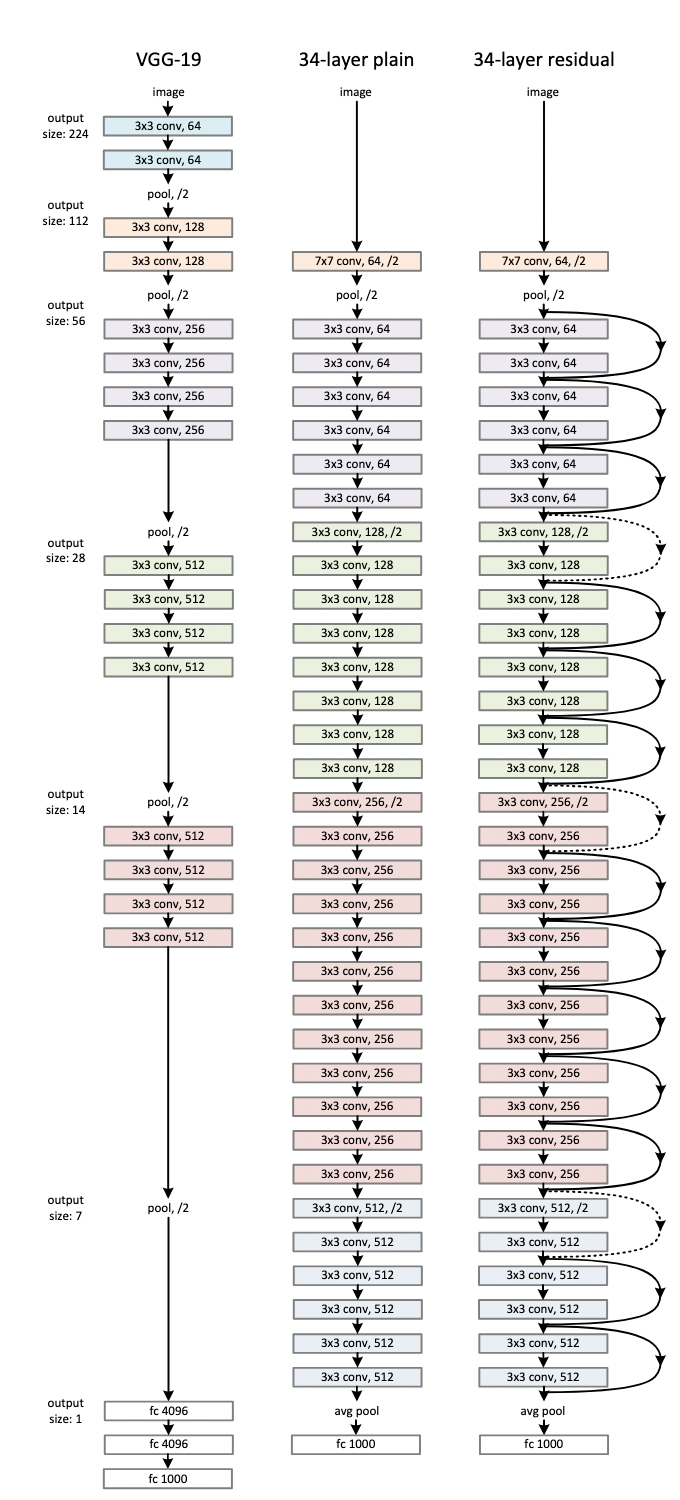
网络架构(Network Architectures)
ResNet的前两层跟之前介绍的GoogLeNet中的一样：
在输出通道数为64、步幅为2的$7 \times 7$卷积层后，接步幅为2的$3 \times 3$的最大汇聚层。
不同之处在于ResNet每个卷积层后增加了批量规范化层。
模型实现(Implementation)
主要介绍对数据处理以及模型的具体参数设置等，不做总结
代码
import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l
class Residual(nn.Module):
def __init__(self, input_channels, num_channels,
use_1x1conv=False, strides=1):
super().__init__()
self.conv1 = nn.Conv2d(input_channels, num_channels,
kernel_size=3, padding=1, stride=strides)
self.conv2 = nn.Conv2d(num_channels, num_channels,
kernel_size=3, padding=1)
if use_1x1conv:
self.conv3 = nn.Conv2d(input_channels, num_channels,
kernel_size=1, stride=strides)
else:
self.conv3 = None
self.bn1 = nn.BatchNorm2d(num_channels)
self.bn2 = nn.BatchNorm2d(num_channels)
def forward(self, X):
Y = F.relu(self.bn1(self.conv1(X)))
Y = self.bn2(self.conv2(Y))
if self.conv3:
X = self.conv3(X)
Y += X
return F.relu(Y)
ResNet
b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
nn.BatchNorm2d(64), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
def resnet_block(input_channels, num_channels, num_residuals,
first_block=False):
blk = []
for i in range(num_residuals):
if i == 0 and not first_block:
blk.append(Residual(input_channels, num_channels,
use_1x1conv=True, strides=2))
else:
blk.append(Residual(num_channels, num_channels))
return blk
b2 = nn.Sequential(*resnet_block(64, 64, 2, first_block=True))
b3 = nn.Sequential(*resnet_block(64, 128, 2))
b4 = nn.Sequential(*resnet_block(128, 256, 2))
b5 = nn.Sequential(*resnet_block(256, 512, 2))
net = nn.Sequential(b1, b2, b3, b4, b5,
nn.AdaptiveAvgPool2d((1,1)),
nn.Flatten(), nn.Linear(512, 10))
每个模块有4个卷积层（不包括恒等映射的$1\times 1$卷积层）。 加上第一个$7\times 7$卷积层和最后一个全连接层，共有18层。 因此，这种模型通常被称为ResNet-18。 通过配置不同的通道数和模块里的残差块数可以得到不同的ResNet模型，例如更深的含152层的ResNet-152。 虽然ResNet的主体架构跟GoogLeNet类似，但ResNet架构更简单，修改也更方便。这些因素都导致了ResNet迅速被广泛使用。
小结
- 学习嵌套函数（nested function）是训练神经网络的理想情况。在深层神经网络中，学习另一层作为恒等映射（identity function）较容易（尽管这是一个极端情况）。
- 残差映射可以更容易地学习同一函数，例如将权重层中的参数近似为零。
- 利用残差块（residual blocks）可以训练出一个有效的深层神经网络：输入可以通过层间的残余连接更快地向前传播。
- 残差网络（ResNet）对随后的深层神经网络设计产生了深远影响。