softmax(1)--算法
分类问题与回归问题有明显的区别,本质是连续和离散的区别,比如我想知道某张照片是猫还是狗,如果模型的输出是一个0.9其实不能代表任何事情,难道越大越像狗吗?(如果是预测婴儿、小孩、青年、老年那还可以用值的大小来界定,但是大多数时候是没有这种自然的大小规律的)。如果模型的输出本身就是离散化的则不会有这个问题,比如模型的输出是两个数,分别代表这个图片是猫或者狗的概率,那就很容易得出预测的结论。
Softmax的模型
从之前的例子可以容易的看出来,softmax的最明显特征就是它的输出是一个向量
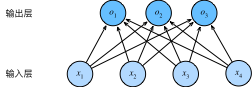
它的数学表达式如下,其实就是一个全联接层: $$ \begin{aligned} o_1 &= x_1 w_{11} + x_2 w_{12} + x_3 w_{13} + x_4 w_{14} + b_1,\\ o_2 &= x_1 w_{21} + x_2 w_{22} + x_3 w_{23} + x_4 w_{24} + b_2,\\ o_3 &= x_1 w_{31} + x_2 w_{32} + x_3 w_{33} + x_4 w_{34} + b_3. \end{aligned} $$
为了更简洁地表达模型,我们仍然使用线性代数符号。 通过向量形式表达为 $\mathbf{o} = \mathbf{W} \mathbf{x} + \mathbf{b}$ , 这是一种更适合数学和编写代码的形式。 由此,我们已经将所有权重放到一个 $3 \times 4$ 矩阵中。 对于给定数据样本的特征 $\mathbf{x}$ , 我们的输出是由权重与输入特征进行矩阵-向量乘法再加上偏置$\mathbf{b}$得到的。
softmax计算
ok现在我们已经有了一个模型,他可以输出一个向量,我们可以规定向量的每个元素代表着某个类别(猫、狗、鸡)的概率,但是还是有问题:
- 直接的全联接层可能会有负数的结果产生,它们的和也不为1,不符合概率学定义
- 同一个输出可能有不同的意义,例如[1,2,3]和[10,20,3],虽然都是3,但是意义完全不同
所以我们需要一个运算,将这个向量变成另一个向量满足概率学的定义:
$$\hat{\mathbf{y}} = \mathrm{softmax}(\mathbf{o})\quad \text{其中}\quad \hat{y}_j = \frac{\exp(o_j)}{\sum_k \exp(o_k)}$$
这里,对于所有的$j$总有$0 \leq \hat{y}_j \leq 1$。
因此,$\hat{\mathbf{y}}$可以视为一个正确的概率分布。
softmax运算不会改变未规范化的预测$\mathbf{o}$之间的大小次序,只会确定分配给每个类别的概率。
因此,在预测过程中,我们仍然可以用下式来选择最有可能的类别。也就是选择概率最大的那个作为预测结果
$$ \operatorname*{argmax}_j \hat y_j = \operatorname*{argmax}_j o_j. $$
尽管softmax是一个非线性函数,但softmax回归的输出仍然由输入特征的仿射变换决定。 因此,softmax回归是一个线性模型(linear model)。
从式子可以看出来,softmax可以理解为一种更先进的求最大值的方法,它的好处有:
- 符合概率学规律
- 指数函数容易求导,所以容易反向传播
- 指数函数能放大差异,e的1次方远远大于1次方
softmax矩阵化
为了提高计算效率并且充分利用GPU,我们通常会对小批量样本的数据执行矢量计算。
假设我们读取了一个批量的样本$\mathbf{X}$,
其中特征维度(输入数量)为$d$,批量大小为$n$。
此外,假设我们在输出中有$q$个类别。
那么小批量样本的特征为$\mathbf{X} \in \mathbb{R}^{n \times d}$,
权重为$\mathbf{W} \in \mathbb{R}^{d \times q}$,
偏置为$\mathbf{b} \in \mathbb{R}^{1\times q}$。
softmax回归的矢量计算表达式为:
$$ \begin{aligned} \mathbf{O} &= \mathbf{X} \mathbf{W} + \mathbf{b}, \\ \hat{\mathbf{Y}} & = \mathrm{softmax}(\mathbf{O}). \end{aligned} $$
相对于一次处理一个样本,
小批量样本的矢量化加快了$\mathbf{X}和\mathbf{W}$的矩阵-向量乘法。
由于$\mathbf{X}$中的每一行代表一个数据样本,
那么softmax运算可以按行(rowwise)执行:
对于$\mathbf{O}$的每一行,我们先对所有项进行幂运算,然后通过求和对它们进行标准化。
$\mathbf{X} \mathbf{W} + \mathbf{b}$的求和会使用广播机制,
小批量的未规范化预测$\mathbf{O}$和输出概率$\hat{\mathbf{Y}}$
都是形状为$n \times q$的矩阵。
交叉熵损失函数
回归模型的损失可以使用均方误差来描述,那这种离散的模型呢则需要交叉熵损失(cross-entropy loss),它的公式如下:
对于任何标签 $\mathbf{y}$ 和模型预测 $\hat{\mathbf{y}}$ ,损失函数为:
$$ l(\mathbf{y}, \hat{\mathbf{y}}) = - \sum_{j=1}^q y_j \log \hat{y}_j. $$
在这个公式中,$\mathbf{y}$ 是一个独热的向量(单分类),也就是说,只有$\mathbf{y}_j=1$,该公式可以写为 $$ l(\mathbf{y}, \hat{\mathbf{y}}) = - y_j \log \hat{y}_j. $$ 就是从多个输出中挑出了真实结果的概率,这个概率越大越好(损失越小)。交叉熵损失函数可以这样理解:让真实标签对应的那个输出更大。
softmax的导数
由于softmax和相关的损失函数很常见,利用softmax的定义,我们得到:
$$ \begin{aligned} l(\mathbf{y}, \hat{\mathbf{y}}) &= - \sum_{j=1}^q y_j \log \frac{\exp(o_j)}{\sum_{k=1}^q \exp(o_k)} \\ &= \sum_{j=1}^q y_j \log \sum_{k=1}^q \exp(o_k) - \sum_{j=1}^q y_j o_j\\ &= \log \sum_{k=1}^q \exp(o_k) - \sum_{j=1}^q y_j o_j. \end{aligned} $$
考虑相对于任何未规范化的预测$o_j$的导数,我们得到:
$$ \partial_{o_j} l(\mathbf{y}, \hat{\mathbf{y}}) = \frac{\exp(o_j)}{\sum_{k=1}^q \exp(o_k)} - y_j = \mathrm{softmax}(\mathbf{o})_j - y_j. $$
换句话说,导数是我们softmax模型分配的概率与实际发生的情况(由独热标签向量表示)之间的差异。