双向循环神经网络

定义

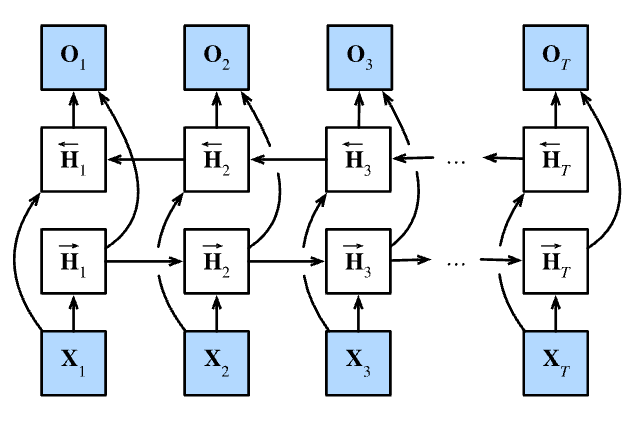
对于任意时间步$t$，给定一个小批量的输入数据 $\mathbf{X}_t \in \mathbb{R}^{n \times d}$ （样本数$n$，每个示例中的输入数$d$）， 并且令隐藏层激活函数为$\phi$。 在双向架构中，我们设该时间步的前向和反向隐状态分别为 $\overrightarrow{\mathbf{H}}_t \in \mathbb{R}^{n \times h}$和 $\overleftarrow{\mathbf{H}}_t \in \mathbb{R}^{n \times h}$， 其中$h$是隐藏单元的数目。 前向和反向隐状态的更新如下：

接下来，将前向隐状态$\overrightarrow{\mathbf{H}}_t$ 和反向隐状态$\overleftarrow{\mathbf{H}}_t$连接起来， 获得需要送入输出层的隐状态$\mathbf{H}_t \in \mathbb{R}^{n \times 2h}$。 在具有多个隐藏层的深度双向循环神经网络中， 该信息作为输入传递到下一个双向层。 最后，输出层计算得到的输出为 $\mathbf{O}_t \in \mathbb{R}^{n \times q}$（$q$是输出单元的数目）：

这里，权重矩阵$\mathbf{W}_{hq} \in \mathbb{R}^{2h \times q}$ 和偏置$\mathbf{b}_q \in \mathbb{R}^{1 \times q}$ 是输出层的模型参数。 事实上，这两个方向可以拥有不同数量的隐藏单元。

双向循环神经网络的错误应用

由于双向循环神经网络使用了过去的和未来的数据， 所以我们不能盲目地将这一语言模型应用于任何预测任务。适合在机器翻译、语言识别等知道上下文的情景使用

小结

• 在双向循环神经网络中，每个时间步的隐状态由当前时间步的前后数据同时决定。
• 双向循环神经网络与概率图模型中的“前向-后向”算法具有相似性。
• 双向循环神经网络主要用于序列编码和给定双向上下文的观测估计。
• 由于梯度链更长，因此双向循环神经网络的训练代价非常高。

• 具体的训练方式，其实就是按照“顺时间、逆时间”进行学习

赞赏支持

微信打赏 支付宝打赏