线性回归(1)--算法
回归(regression)是能为一个或多个自变量与因变量之间关系建模的一类方法。在自然科学和社会科学领域,回归经常用来表示输入和输出之间的关系。
在机器学习领域中的大多数任务通常都与预测(prediction)有关。 当我们想预测一个数值时,就会涉及到回归问题。 常见的例子包括:预测价格(房屋、股票等)、预测住院时间(针对住院病人等)、 预测需求(零售销量等)。 但不是所有的预测都是回归问题。
线性回归基本元素
为了解释线性回归,我们举一个实际的例子: 我们希望根据房屋的面积(平方英尺)和房龄(年)来估算房屋价格(美元)。 为了开发一个能预测房价的模型,我们需要收集一个真实的数据集。 这个数据集包括了房屋的销售价格、面积和房龄。
在机器学习的术语中,该数据集称为训练数据集(training data set) 或训练集(training set)。 每行数据(比如一次房屋交易相对应的数据)称为样本(sample), 也可以称为数据点(data point)或数据样本(data instance)。
我们把试图预测的目标(比如预测房屋价格)称为标签(label)或目标(target)。 预测所依据的自变量(面积和房龄)称为特征(feature)或协变量(covariate)。
通常,我们使用$n$来表示数据集中的样本数。 对索引为 $i$ 的样本,其输入表示为 $\mathbf{x}^{(i)} = [x_1^{(i)}, x_2^{(i)}]^\top$ , 其对应的标签是 $y^{(i)}$ 。
线性模型
线性假设是指目标(房屋价格)可以表示为特征(面积和房龄)的加权和,如下面的式子:
$$\mathrm{price} = w_{\mathrm{area}} \cdot \mathrm{area} + w_{\mathrm{age}} \cdot \mathrm{age} + b.$$
而在机器学习领域,我们通常使用的是高维数据集,建模时采用线性代数表示法会比较方便。 当我们的输入包含$d$个特征时,我们将预测结果 $\hat{y}$(通常使用“尖角”符号表示$y$的估计值)表示为:
$$\hat{y} = w_1 x_1 + … + w_d x_d + b.$$
将所有特征放到向量 $\mathbf{x} \in \mathbb{R}^d$ 中, 并将所有权重放到向量 $\mathbf{w} \in \mathbb{R}^d$ 中, 我们可以用点积形式来简洁地表达模型:
$$\hat{y} = \mathbf{w}^\top \mathbf{x} + b.$$
向量 $\mathbf{x}$ 对应于单个数据样本的特征。 用符号表示的矩阵 $\mathbf{X} \in \mathbb{R}^{n \times d}$ 可以很方便地引用我们整个数据集的 $n$ 个样本。 其中, $\mathbf{X}$ 的每一行是一个样本,每一列是一种特征。
对于特征集合 $\mathbf{X}$ ,预测值 $\hat{\mathbf{y}} \in \mathbb{R}^n$ 可以通过矩阵-向量乘法表示为: $${\hat{\mathbf{y}}} = \mathbf{X} \mathbf{w} + b$$
线性回归的目标是找到一组权重向量 $\mathbf{w}$ 和偏置 $b$ :
当给定从 $\mathbf{X}$ 的同分布中取样的新样本特征时,
这组权重向量和偏置能够使得新样本预测标签的误差尽可能小
在这个实际的例子中,我们的线性模型表达式如下:
$$\hat{y} = w_1 x_1 + w_2 x_2 + b.$$
在开始寻找最好的模型参数(model parameters) $\mathbf{w}$ 和 $b$ 之前, 我们还需要两个东西:
- 一种模型质量的度量方式;
- 一种能够更新模型以提高模型预测质量的方法。
损失函数
在我们开始考虑如何用模型拟合(fit)数据之前,我们需要确定一个拟合程度的度量。
损失函数(loss function)能够量化目标的实际值与预测值之间的差距。
通常我们会选择非负数作为损失,且数值越小表示损失越小,完美预测时的损失为0。
回归问题中最常用的损失函数是平方误差函数。
当样本 $i$ 的预测值为 $\hat{y}^{(i)}$ ,其相应的真实标签为 $y^{(i)}$ 时,
平方误差可以定义为以下公式:
$$l^{(i)}(\mathbf{w}, b) = \frac{1}{2} \left(\hat{y}^{(i)} - y^{(i)}\right)^2.$$
常数 $\frac{1}{2}$ 不会带来本质的差别,但这样在形式上稍微简单一些(因为当我们对损失函数求导后常数系数为1)。
由于训练数据集并不受我们控制,所以经验误差只是关于模型参数的函数。
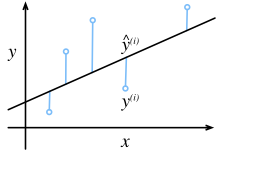
由于平方误差函数中的二次方项, 估计值 $\hat{y}^{(i)}$ 和观测值 $y^{(i)}$ 之间较大的差异将导致更大的损失。 为了度量模型在整个数据集上的质量,我们需计算在训练集 $n$ 个样本上的损失均值(也等价于求和)。
$$ L(\mathbf{w}, b) =\frac{1}{n}\sum_{i=1}^n l^{(i)}(\mathbf{w}, b) =\frac{1}{n} \sum_{i=1}^n \frac{1}{2}\left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right)^2. $$
优化方法
解析解
线性回归的解可以用一个公式简单地表达出来, 这类解叫作解析解(analytical solution)。 首先,我们将偏置 $b$ 合并到参数 $\mathbf{w}$ 中,合并方法是在包含所有参数的矩阵中附加一列。 我们的预测问题是最小化 $|\mathbf{y} - \mathbf{X}\mathbf{w}|^2$ 。 这在损失平面上只有一个临界点,这个临界点对应于整个区域的损失极小点。 将损失关于 $\mathbf{w}$ 的导数设为0,得到解析解: $$\mathbf{w}^* = (\mathbf X^\top \mathbf X)^{-1}\mathbf X^\top \mathbf{y}.$$
像线性回归这样的简单问题存在解析解,但并不是所有的问题都存在解析解。 解析解可以进行很好的数学分析,但解析解对问题的限制很严格,导致它无法广泛应用在深度学习里。
数值解(小批量随机梯度下降)
在每次迭代中,我们首先随机抽样一个小批量$\mathcal{B}$, 它是由固定数量的训练样本组成的。 然后,我们计算小批量的平均损失关于模型参数的导数(也可以称为梯度)。 最后,我们将梯度乘以一个预先确定的正数$\eta$,并从当前参数的值中减掉。
我们用下面的数学公式来表示这一更新过程($\partial$表示偏导数):
$$(\mathbf{w},b) \leftarrow (\mathbf{w},b) - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \partial_{(\mathbf{w},b)} l^{(i)}(\mathbf{w},b).$$
总结一下,算法的步骤如下:
- 初始化模型参数的值,如随机初始化;
- 从数据集中随机抽取小批量样本且在负梯度的方向上更新参数,并不断迭代这一步骤。
对于平方损失和仿射变换,我们可以明确地写成如下形式:
$$\begin{aligned} \mathbf{w} &\leftarrow \mathbf{w} - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \partial_{\mathbf{w}} l^{(i)}(\mathbf{w}, b) = \mathbf{w} - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \mathbf{x}^{(i)} \left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right),\\ b &\leftarrow b - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \partial_b l^{(i)}(\mathbf{w}, b) = b - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right). \end{aligned}$$
$|\mathcal{B}|$ 表示每个小批量中的样本数,这也称为批量大小(batch size)。
$\eta$ 表示学习率(learning rate)。
批量大小和学习率的值通常是手动预先指定,而不是通过模型训练得到的。
这些可以调整但不在训练过程中更新的参数称为超参数(hyperparameter)。
调参(hyperparameter tuning)是选择超参数的过程。
超参数通常是我们根据训练迭代结果来调整的,
而训练迭代结果是在独立的验证数据集(validation dataset)上评估得到的。
线性回归的表示⽅法
神经网络
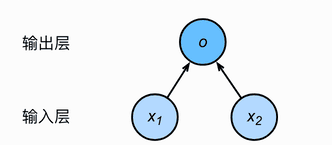
根据线性回归的形式,很容易看出来它就是一个单层的神经网络:
矢量计算
使用向pytorch的向量运算效率很高,因此,应该尽量将计算表示成向量运算的形式:
 其中梯度可表示为:
其中梯度可表示为: