计算图
为各类神经网络计算提供统一的描述
计算图提出
计算图又叫数据流图,用一个有向无环图表示计算过程。边表示数据(data),点表示算子(Operator)。
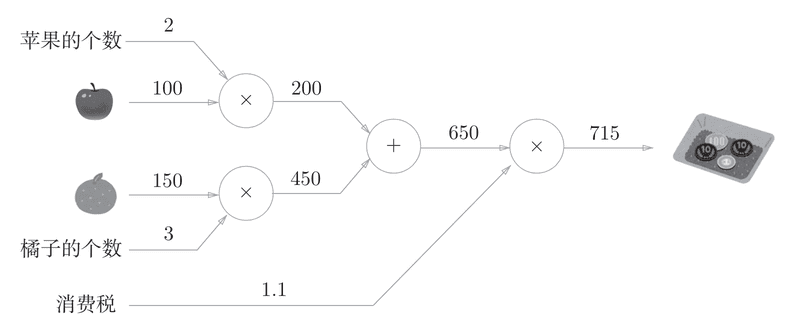
- 如何在系统中统一表示神经网络?
- 如何实现自动求导?
- 如何对神经网络进行化简、合并、变换?
- 如何规划基本计算单元在加速器上高速执行?
- 如何进行内存预分配和管理?
- 基本处理单元派发到特定后端执行?
作为一个单纯的使用者,我认为能浅浅思考一下前两个问题就可以了。AI框架有很多种,在底层是不是应该有一个通用表示方法呢,这个表示方法肯定要满足精确性和“单元解释性”,也就是说它得是数学表达式。
在AI求导的时候,用数值估计的方式会损失精度并且计算开销太大了(f(x+h)-f(x)/h),用纯数学表达又会遇到某些函数没有解析导函数的情况(relu、gate)
以我目前的理解,计算图是一种AI模型的通用表示,并且框架可以利用它存储前向的信息从而快速求导的工具
或者说:为各类神经网络计算提供统一的描述
计算图与自动微分
自动微分:由原子操作构成的复杂前向计算程序,关注自动生成高效的反向计算程序
为什么需要自动微分
我们在训练大多数AI模型的时候,其实目标就一个,减少loss,说白了就是找到这个loss的鞍点,可以说,训练流程核心就是求导
| 名称 | 特点 | 优点 | 缺点 |
|---|---|---|---|
| 符号微分(Symbolic Differentiation) | 通过求导法则和导数变换公式,精确计算函数的导数 | 精确数值结果 | 表达式膨胀 |
| 数值微分(Numerical Differentiation) | 使用有限差分进行近似导数 | 容易实现 | 计算结果不精确、计算复杂度高、对 ℎ 的要求高 |
| 自动微分(Auto Differentiation) | 所有数值计算都由有限的基本运算组成、基本运算的导数表达式是已知的、通过链式法则将数值计算各部分组合成整体 | 计算机友好 |
通过以上表格,选择自动微分是合理的。
如何自动微分/反向传播
考虑如下表达式:
$$𝑓(𝑥_1,𝑥_2 )=ln(𝑥_1 )+𝑥_1 𝑥_2−sin(𝑥_2)$$
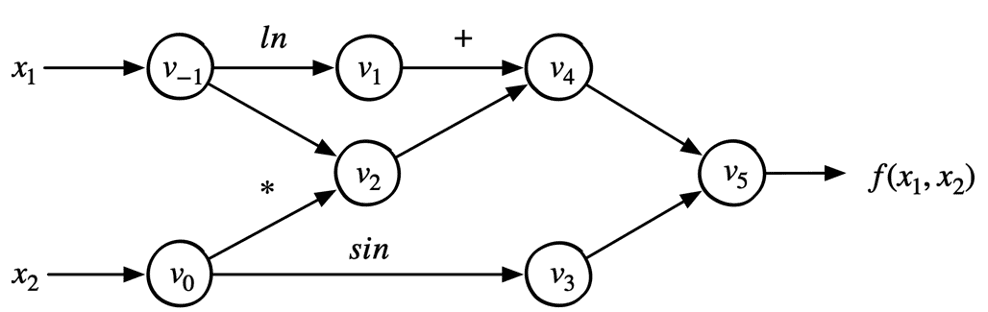

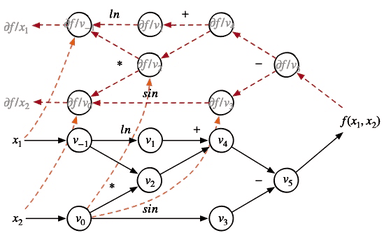

为了更快的计算,我们需要用到矩阵表示:
之前我们了解了输入输出都是向量的函数的偏导数表示:雅克比矩阵
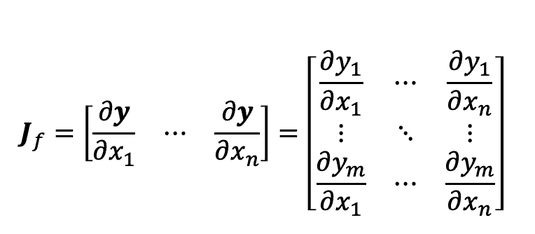
在pytorch中规定loss是个标量,后一层损失函数对当前层输出的导数可以表示为
$$\boldsymbol{v}=[\frac{\partial loss}{\partial y_1},…,\frac{\partial loss}{\partial y_m}]^\top$$
将雅可比矩阵和上面的向量相乘,就得到了再前一层的导数【此例为第二层,也就是x】:
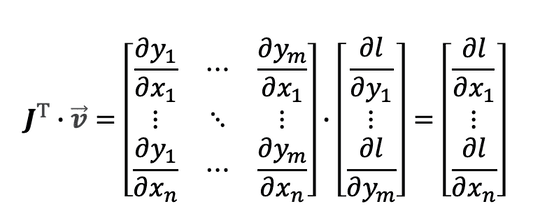
如果网络再深,也不过是多做几次矩阵乘法,这对计算机来说是效率很高的!