多通道

多通道输入

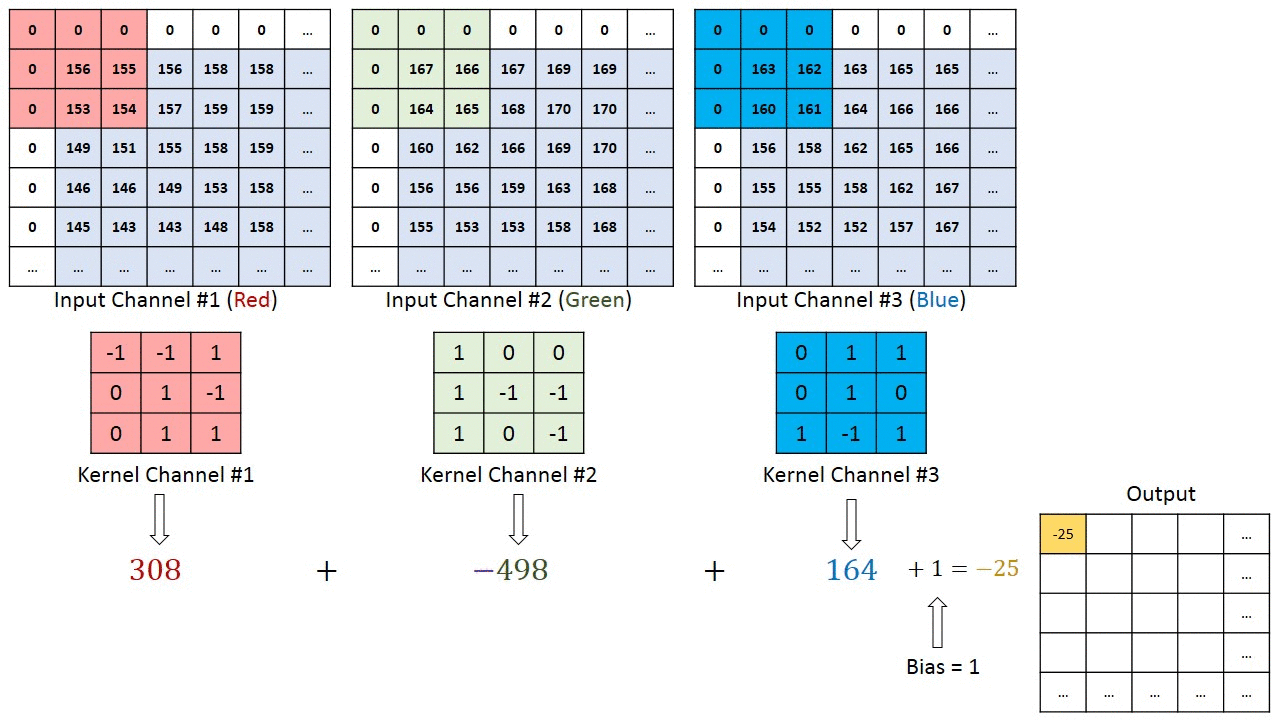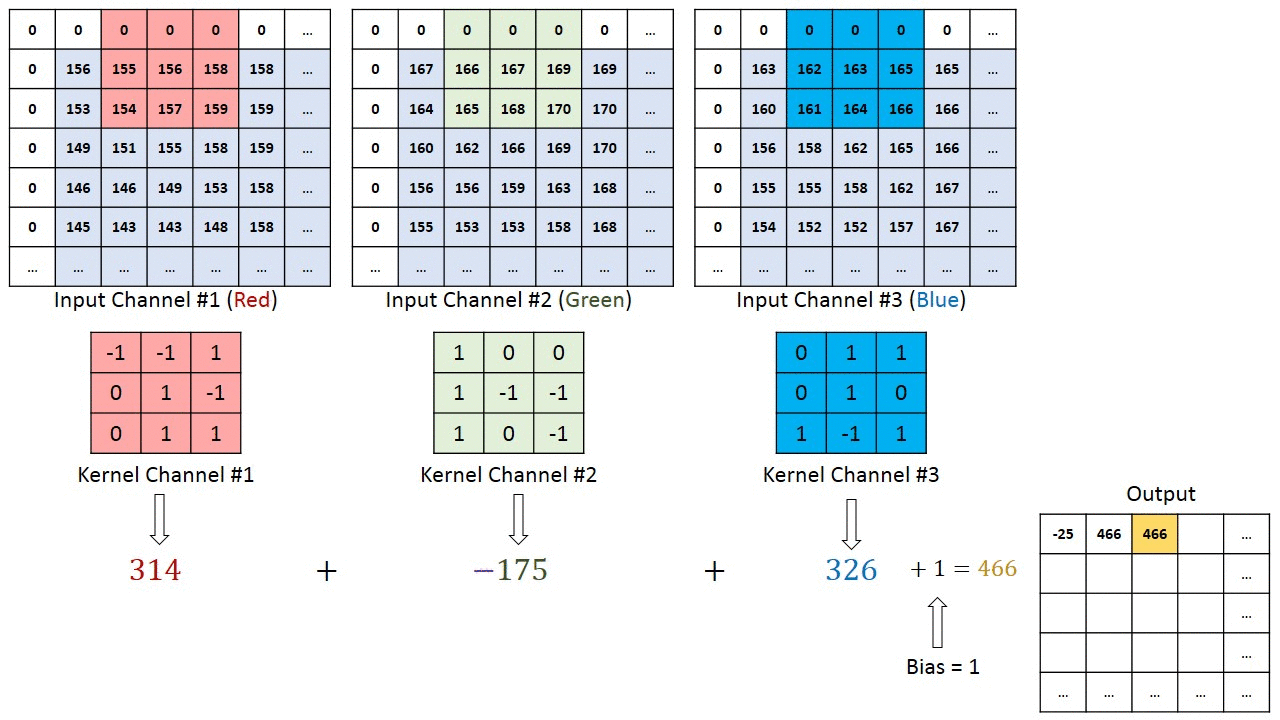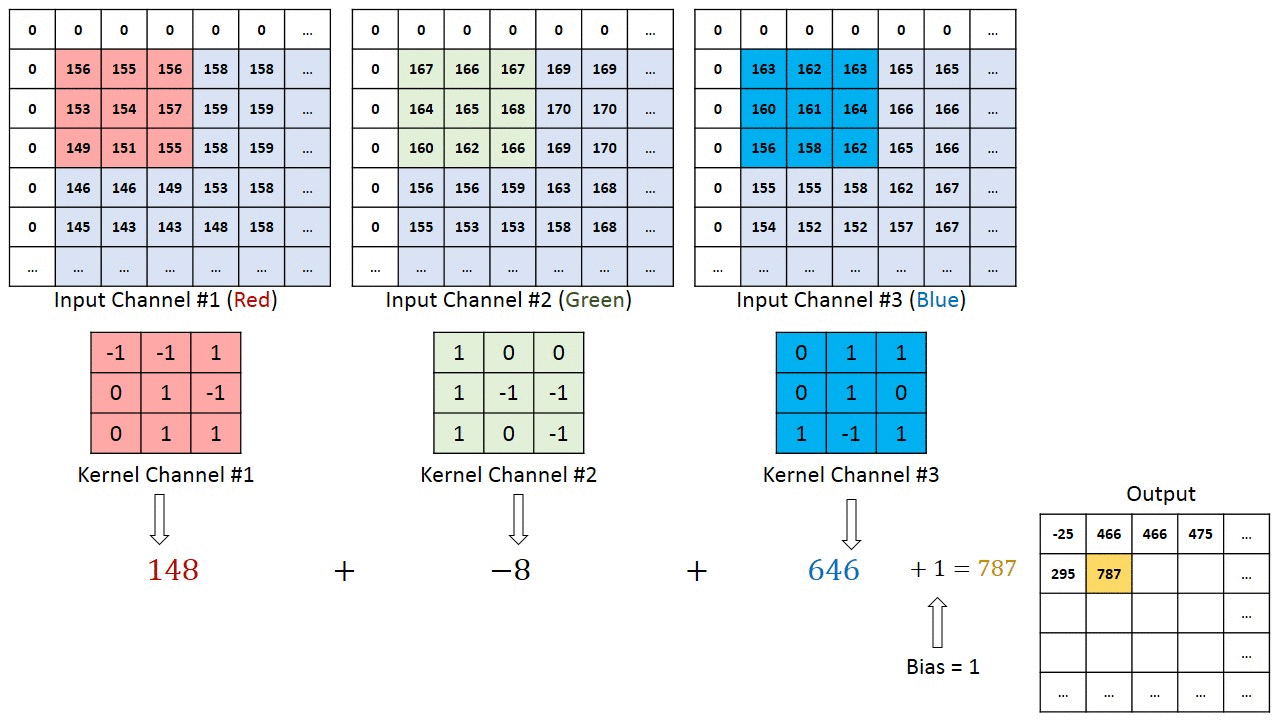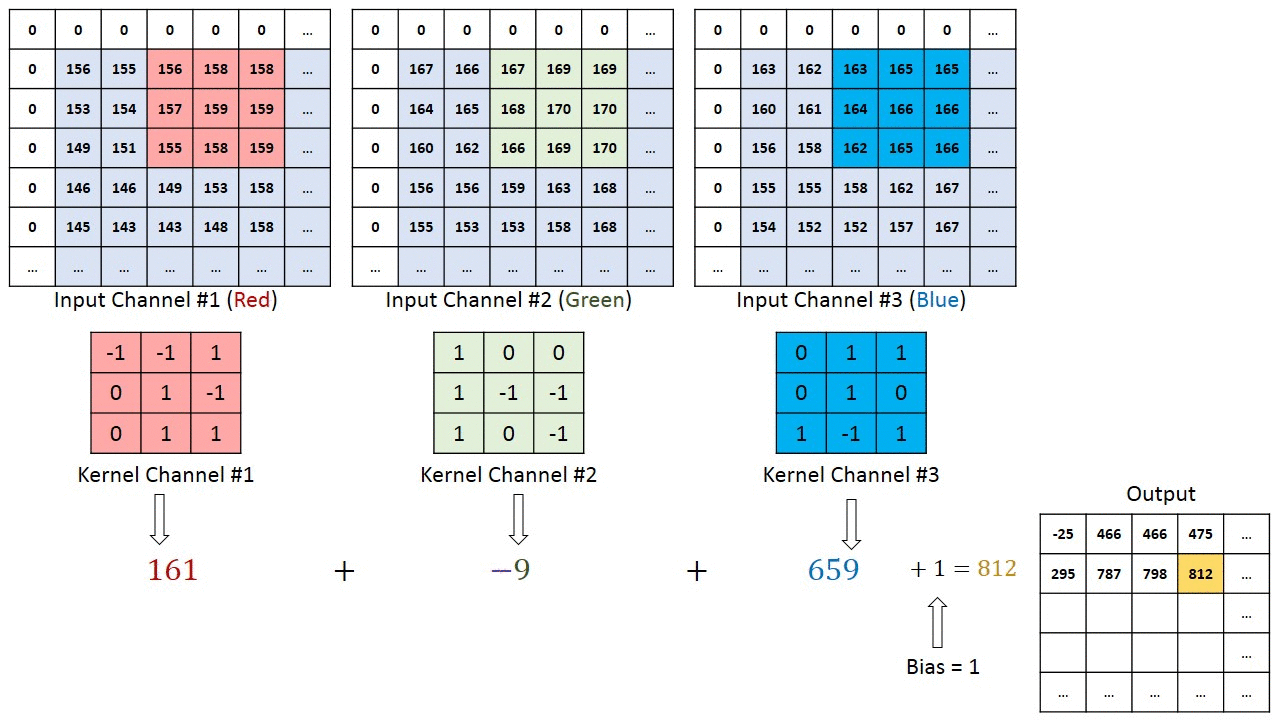
然而，当$c_i>1$时，我们卷积核的每个输入通道将包含形状为$k_h\times k_w$的张量。将这些张量$c_i$连结在一起可以得到形状为$c_i\times k_h\times k_w$的卷积核。由于输入和卷积核都有$c_i$个通道，我们可以对每个通道输入的二维张量和卷积核的二维张量进行互相关运算，再对通道求和（将$c_i$的结果相加）得到二维张量。这是多通道输入和多输入通道卷积核之间进行二维互相关运算的结果。

def corr2d_multi_in(X, K):
    # 先遍历“X”和“K”的第0个维度（通道维度），再把它们加在一起
    return sum(d2l.corr2d(x, k) for x, k in zip(X, K))

多通道输出

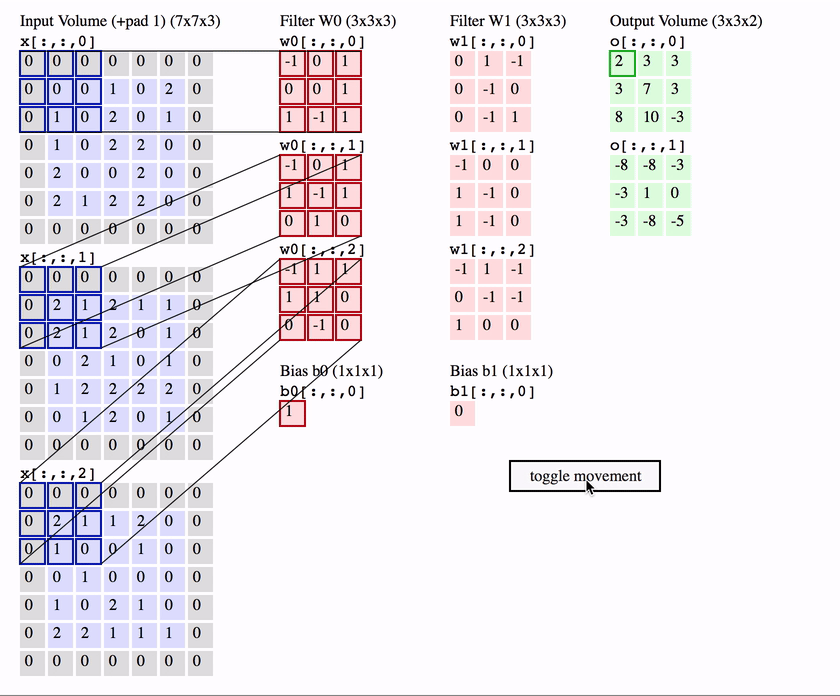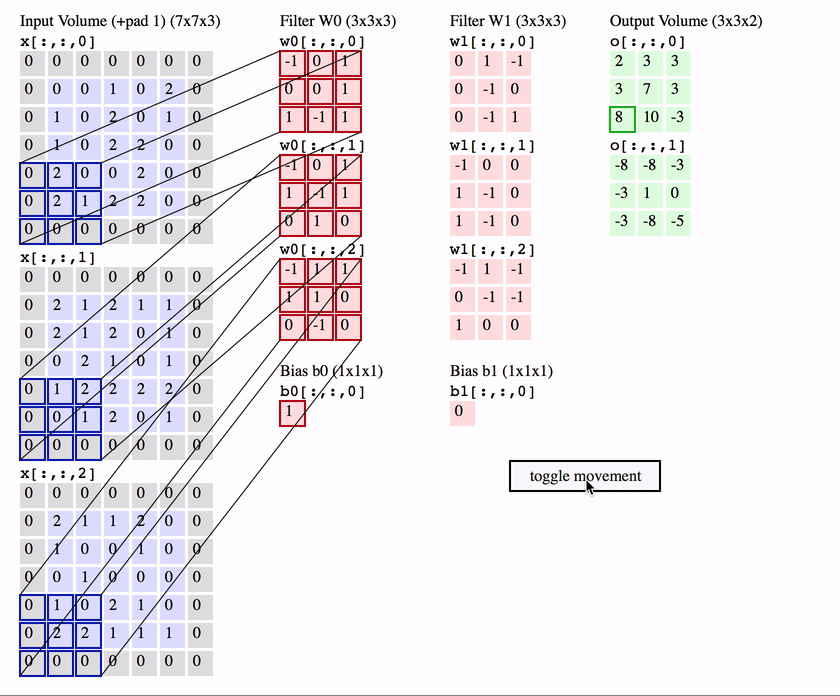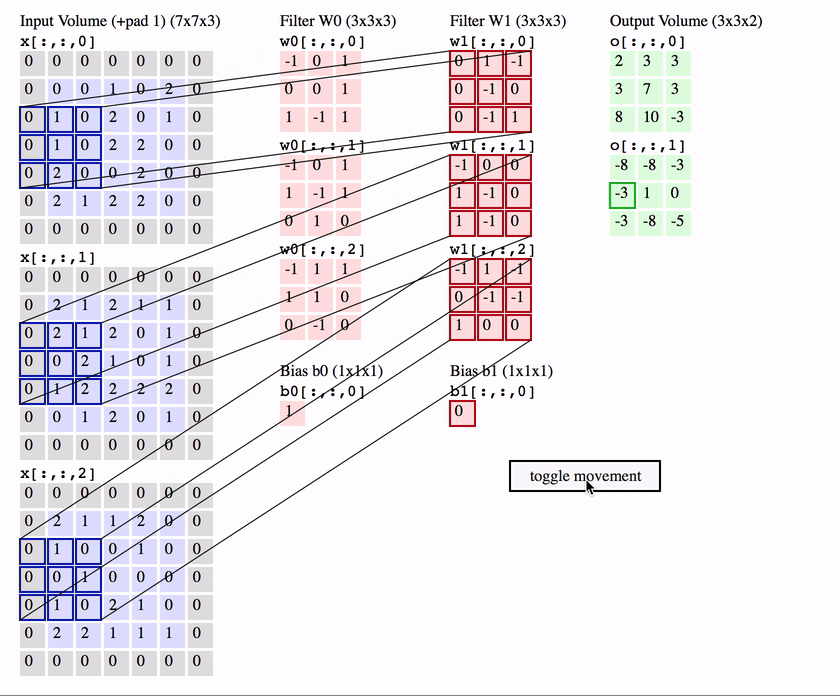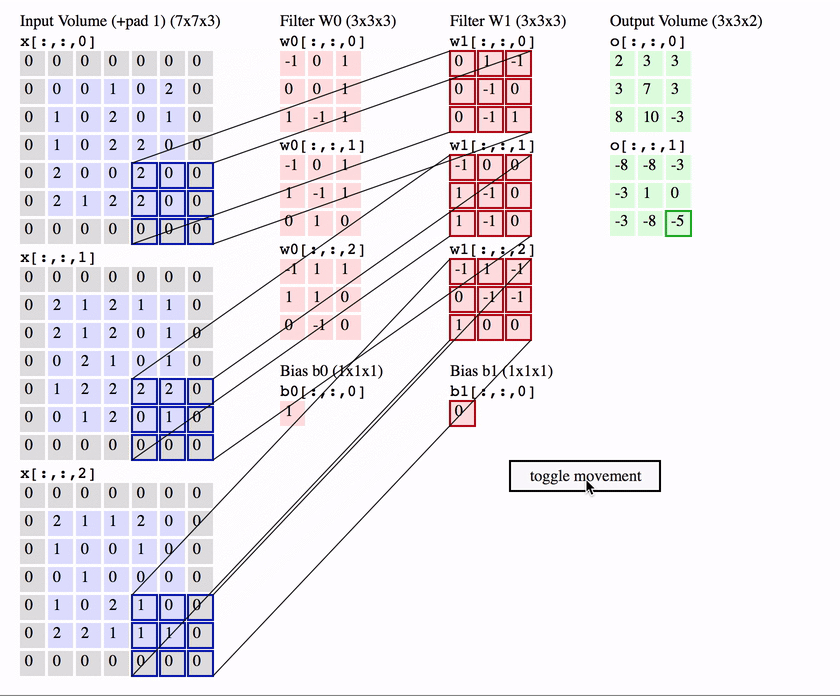
用$c_i$和$c_o$分别表示输入和输出通道的数目，并让$k_h$和$k_w$为卷积核的高度和宽度。为了获得多个通道的输出，我们可以为每个输出通道创建一个形状为$c_i\times k_h\times k_w$的卷积核张量，这样卷积核的形状是$c_o\times c_i\times k_h\times k_w$。在互相关运算中，每个输出通道先获取所有输入通道，再以对应该输出通道的卷积核计算出结果。

def corr2d_multi_in_out(X, K):
    # 迭代“K”的第0个维度，每次都对输入“X”执行互相关运算。
    # 最后将所有结果都叠加在一起
    return torch.stack([corr2d_multi_in(X, k) for k in K], 0)

1x1卷积核

因为使用了最小窗口，$1\times 1$卷积失去了卷积层的特有能力——在高度和宽度维度上，识别相邻元素间相互作用的能力。 其实$1\times 1$卷积的唯一计算发生在通道上。

def corr2d_multi_in_out_1x1(X, K):
    c_i, h, w = X.shape
    c_o = K.shape[0]
    X = X.reshape((c_i, h * w))
    K = K.reshape((c_o, c_i))
    # 全连接层中的矩阵乘法
    Y = torch.matmul(K, X)
    return Y.reshape((c_o, h, w))

小结

• 多输入多输出通道可以用来扩展卷积层的模型。
• 当以每像素为基础应用时，$1\times 1$卷积层相当于全连接层。
• $1\times 1$卷积层通常用于调整网络层的通道数量和控制模型复杂性。

赞赏支持

微信打赏 支付宝打赏