vgg
目录
VGG块
经典卷积神经网络的基本组成部分是下面的这个序列:
- 带填充以保持分辨率的卷积层;
- 非线性激活函数,如ReLU;
- 汇聚层,如最大汇聚层。
而一个VGG块与之类似,由一系列卷积层组成,后面再加上用于空间下采样的最大汇聚层。在最初的VGG论文中 作者使用了带有$3\times3$卷积核、填充为1(保持高度和宽度)的卷积层,和带有$2 \times 2$汇聚窗口、步幅为2(每个块后的分辨率减半)的最大汇聚层。在下面的代码中,我们定义了一个名为vgg_block的函数来实现一个VGG块。
VGG结构
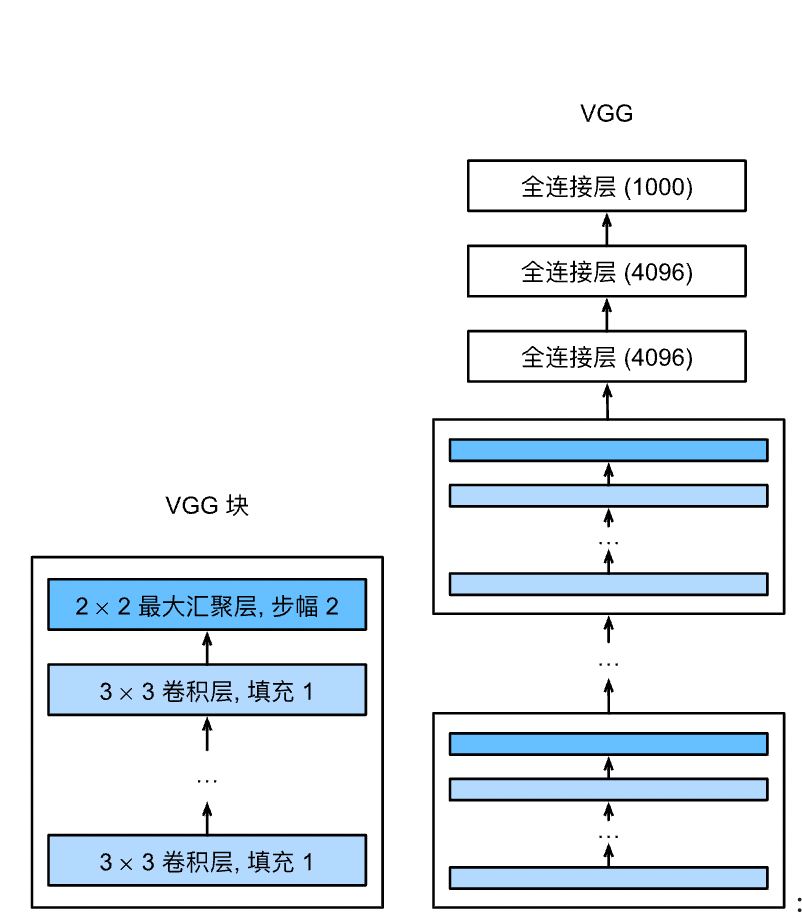
vgg块
import torch
from torch import nn
from d2l import torch as d2l
def vgg_block(num_convs, in_channels, out_channels):
layers = []
for _ in range(num_convs):
layers.append(nn.Conv2d(in_channels, out_channels,
kernel_size=3, padding=1))
layers.append(nn.ReLU())
in_channels = out_channels
layers.append(nn.MaxPool2d(kernel_size=2,stride=2))
return nn.Sequential(*layers)
以上函数中三个参数,分别对应于卷积层的数量num_convs、输入通道的数量in_channels 和输出通道的数量out_channels.
在循环中,添加指定数量的卷积层,最后添加一个maxpool层,这里的*[]告诉python将列表里的元素按照参数传给函数
vgg网络
原始VGG网络有5个卷积块,其中前两个块各有一个卷积层,后三个块各包含两个卷积层。 第一个模块有64个输出通道,每个后续模块将输出通道数量翻倍,直到该数字达到512。由于该网络使用8个卷积层和3个全连接层,因此它通常被称为VGG-11。
conv_arch = ((1, 64), (1, 128), (2, 256), (2, 512), (2, 512))
def vgg(conv_arch):
conv_blks = []
in_channels = 1
# 卷积层部分
for (num_convs, out_channels) in conv_arch:
conv_blks.append(vgg_block(num_convs, in_channels, out_channels))
in_channels = out_channels
return nn.Sequential(
*conv_blks, nn.Flatten(),
# 全连接层部分
nn.Linear(out_channels * 7 * 7, 4096), nn.ReLU(), nn.Dropout(0.5),
nn.Linear(4096, 4096), nn.ReLU(), nn.Dropout(0.5),
nn.Linear(4096, 10))
net = vgg(conv_arch)
小结
- VGG-11使用可复用的卷积块构造网络。不同的VGG模型可通过每个块中卷积层数量和输出通道数量的差异来定义。
- 块的使用导致网络定义的非常简洁。使用块可以有效地设计复杂的网络。
- 在VGG论文中,Simonyan和Ziserman尝试了各种架构。特别是他们发现深层且窄的卷积(即$3 \times 3$)比较浅层且宽的卷积更有效。